شیمی دبیرستان استان خوزستان

شیمی

شیمی دبیرستان استان خوزستان

شیمی

لگاریتم

برای لگاریتم گرفتن بدون استفاده از ماشین حساب ،اعداد بنا بر رقم اولشون به سه دسته تقسیم می شن
("." نشان دهنده ی ممیزه)

***********************
الف) اگر رقم اول عدد 1 باشه :
تعداد ارقام بعد از ممیز - {1. (1 - تعداد ارقام)} = لگاریتم

به طور مثال لگاریتم عدد 10542 با این روش می شه
4.1 =0 -{ 1.(1 - 5 )}
که با مقدار واقعیش یعنی 4.023 اختلاف کمی داره.

یا مثلا لگاریتم عدد 0.123 می شه
0.9 - = 3 - { 1 . (1 - 3)}
که مقدار واقعیش هست 91 .0 -

************************

ب ) اگر رقم اول از اعداد 2 تا 7 باشه :

تعداد ارقام بعد از ممیز - (2 + رقم اول ) . (1 - تعداد ارقام) = لگاریتم

مثلا لگاریتم عدد 3542
5 .3 = 0 - { (2 + 3) .(1- 4) }
مقدار واقعیش 55. 3

***********************

ج) و در صورتیکه رقم اول از اعداد 8 و 9 باشد:

تعداد ارقام بعد از ممیز - 9 . (1 - تعداد ارقام) = لگاریتم

به عنوان مثال 8542
9. 3 = 9 . (1 - 4)
و مقدار واقعیش هست 3.93

برای محاسبه آنتی لگاریتم رابطه کلی زیر را داریم:

$\log _{b}a=c\rightarrow a=b^{c}$

محاسبه ریشه اعداد :

در حالت کلی فرمول زیر را داریم:

$\sqrt[n]{a^{n}+b}=a+\frac{b}{na^{n-1}}$

لگاریتم ضرب را به جمع تبدیل می کند.
لگاریتم تقسیم را به منها تبدیل می کند.
لگاریتم توان را به ضرب می برد.

ضرب، تقسیم، توان، ریشه[ویرایش]
لگاریتم حاصل ضرب چند عدد برابر است با مجموع لگاریتم‌های تک تک آن عددها. لگاریتم نسبت دو عدد (تقسیم) برابر است با تفاضل لگاریتم آن دو عدد. لگاریتم توان p ام یک عدد برابر است با p برابر لگاریتم آن عدد. لگاریتم ریشهٔ p ام یک عدد برابر است با لگاریتم آن عدد تقسیم بر p. جدول زیر قوانین لگاریتم را همراه با یک نمونه نشان داده‌است:
رابطه نمونه
ضرب $\log_b(x y) = \log_b (x) + \log_b (y) \,$ $\log_3 (243) = \log_3(9 \times 27) = \log_3 (9) + \log_3 (27) = 2 + 3 = 5 \,$
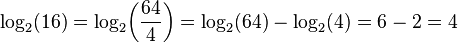تقسیم $\log_b \!\left(\frac x y \right) = \log_b (x) - \log_b (y) \,$ $\log_2 (16) = \log_2 \!\left (\frac{64}{4} \right) = \log_2 (64) - \log_2 (4) = 6 - 2 = 4$
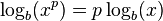توان $\log_b(x^p) = p \log_b (x) \,$ $\log_2 (64) = \log_2 (2^6) = 6 \log_2 (2) = 6 \,$
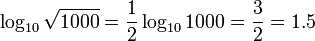ریشه $\log_b \sqrt[p]{x} = \frac {\log_b (x)} p \,$ $\log_{10} \sqrt{1000} = \frac{1}{2}\log_{10} 1000 = \frac{3}{2} = 1.5$
تغییر پایه[ویرایش]
می‌توان 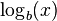$\log_b(x)$ را به صورت غیر مستقیم با گرفتن لگاریتم x و b در یک پایهٔ دلخواه مانند k بدست آورد، به این ترتیب که:
$\log_b(x) = \frac{\log_k(x)}{\log_k(b)}. \,$
بیشتر ماشین حساب‌هایی که در دسترس اند لگاریتم را تنها در مبنای ۱۰ و عدد نپر^[۳] محاسبه می‌کنند و لگاریتم در پایه‌های دیگر را به کمک رابطهٔ بالا محاسبه می‌کنند:
$\log_b (x) = \frac{\log_{10} (x)}{\log_{10} (b)} = \frac{\log_{e} (x)}{\log_{e} (b)}. \,$
همچنین اگر عددی مانند x و مقدار لگاریتم آن را در یک مبنای نامشخص b داشته باشیم 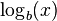$\log_b (x)$ حال می‌توان مبنای نامشخص b را به ترتیب زیر محاسبه کرد:
$b = x^\frac{1}{\log_b(x)}.$

	رابطه	نمونه
ضرب	$\log_b(x y) = \log_b (x) + \log_b (y) \,$	$\log_3 (243) = \log_3(9 \times 27) = \log_3 (9) + \log_3 (27) = 2 + 3 = 5 \,$
تقسیم	$\log_b \!\left(\frac x y \right) = \log_b (x) - \log_b (y) \,$	$\log_2 (16) = \log_2 \!\left (\frac{64}{4} \right) = \log_2 (64) - \log_2 (4) = 6 - 2 = 4$
توان	$\log_b(x^p) = p \log_b (x) \,$	$\log_2 (64) = \log_2 (2^6) = 6 \log_2 (2) = 6 \,$
ریشه	$\log_b \sqrt[p]{x} = \frac {\log_b (x)} p \,$	$\log_{10} \sqrt{1000} = \frac{1}{2}\log_{10} 1000 = \frac{3}{2} = 1.5$